Податливость. Характеристики оптического стола
Основной целью хорошо спроектированного оптического стола является устранение относительного движения между любыми двумя (или более) компонентами на поверхности оптического стола. Однако прежде чем обсуждать конструкцию оптических столов, необходимо изучить основную теорию вибраций и номенклатуру, обычно используемую для обсуждения вибраций столешницы: податливость, вибрации, резонанс и демпфирование.
Податливость
При проектировании оптической столешницы необходимо решить стандартную задачу о деформации тела или структуры в ответ на внешнее воздействие сил. Силы могут быть статическими, такими как провисание столешницы из-за большой массы, помещаемой на столе. Силы могут быть динамическими, такими как акустические колебания в воздухе, вибрации небольшого двигателя, расположенного на верхней части оптического стола, или вибрация, передаваемая от здания на оптический стол через опоры оптического стола.
Определение податливости
Наиболее широко используемая функция для вибрационного отклика оптического стола является податливость. В случае статической постоянной силы податливость определяется как отношение смещения к величине приложенной силы. В случае динамически изменяющейся силы (вибрации) податливость определяется как отношение возбуждаемой амплитуды колебаний к амплитуде силы, вызывающей вибрацию.
Любой прогиб столешницы подтверждается изменением относительного положения компонентов, установленных на поверхности стола. Следовательно, по определению, чем ниже значение податливости, тем ближе оптический стол к решению основной цели проектирования оптического стола, которая сводит к минимуму прогиб. Податливость зависит от частоты и измеряется в единицах смещения на единицу силы (в метрах на ньютон).
Кривые податливости
Чтобы понять термин "податливость", рассмотрим гипотетическую систему только с одной вибрационной степенью свободы (то есть, систему только с одним направлением деформации). Например, эта конструкция может представлять собой стальной стержень, который прочно закреплен на одном конце и способен вибрировать только в одном направлении, как показано на рисунке 1. Этот стержень может отклоняться только в вертикальном направлении.
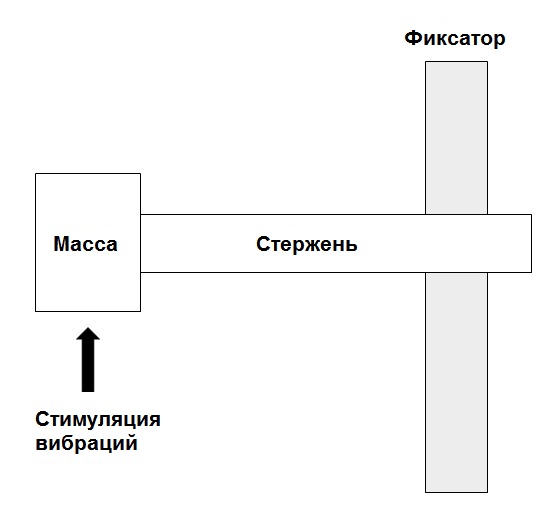
Рисунок 1: Простая система с одной степенью свободы: ограниченный стержень, вибрирующий только в одной плоскости
Все периодические колебания могут быть выражены как комбинации функций синуса и косинуса с соответствующей амплитудой, частотой и фазой. Следовательно, когда синусоидальная вибрация применяется к стержню, общее уравнение движения имеет вид
![]()
где левая часть относится к системе, подвергающейся внешнему воздействию, а правая часть уравнения относится к функции воздействия.
![]() ,
, ![]() и
и ![]() - ускорение, скорость и смещение перемещаемой массы (m) соответственно, а c и k - параметры демпфирования и жесткости соответственно.
- ускорение, скорость и смещение перемещаемой массы (m) соответственно, а c и k - параметры демпфирования и жесткости соответственно.
Сила F синусоидально изменяется с частотой f и максимальной амплитудой F0. Общее выражение податливости такой системы:
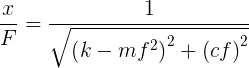
Если мы переформулируем вышеприведенное уравнение словами,
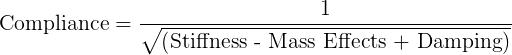
График зависимости податливости от частоты (как видно на рисунке 2) показывает, что податливость жесткого тела можно разделить на три области: жесткость, резонанс и массовые эффекты.
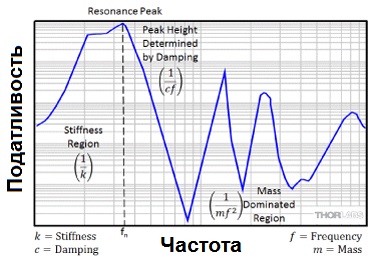
Рисунок 2: Зависимость податливости от частоты для системы с одной степенью свободы
Податливость на низких частотах – жесткость
На нулевых и низких частотах массовые эффекты и коэффициенты демпфирования фактически равны нулю, поэтому податливость хорошо аппроксимируется с помощью коэффициента жесткости 1 / k. Когда низкочастотная вынуждающая вибрация воздействует на неприкрепленный конец стержня, он изгибается в ответ. Величина прогиба определяется жесткостью стержня, которая в конечном итоге зависит от его формы, модуля упругости при растяжении (модуля Юнга) материала стержня, а также от способа установки и / или крепления стержня.
Любое твердое тело имеет фиксированное равновесие или геометрию покоя. Равновесная геометрия соответствует минимуму потенциальной энергии объекта. Когда силы приложены к твердому телу, оно может деформироваться. Потенциальная энергия тела увеличивается, и в результате возникает сила, которая восстанавливает тело до его равновесной формы.
Рассмотрим ситуацию, когда стержень отклонился от своего положения равновесия, а затем был отпущен. Восстанавливающая сила действует, чтобы вернуть стержень в его положение равновесия. Однако, даже если восстанавливающая сила на стержне будет равна нулю, когда он достигнет своего равновесного положения, инерция заставит его перескочить это положение. В результате стержень будет колебаться вокруг своего положения равновесия. Колебание стержня является примером простого гармонического осциллятора. Колебание происходит с характерной частотой fn, называемой резонансной частотой, определяемой как
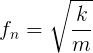
где fn - резонансная частота колебаний, m - масса, движущаяся во время колебаний, а k – коэффициент жесткости пружины, которая связана с формой стержня и модулем Юнга материала, из которого стержень изготовлен. При отсутствии демпфирования это колебание будет существовать вечно.
В реальной системе, такой как оптический стол, резонансные колебания редко могут быть приближены к гармоническим колебаниям с такой простой математикой; однако приведенные выше аргументы все же могут дать общее понимание.
Податливость в резонансе
Подставляем решение последнего уравнения для m в формулу податливости
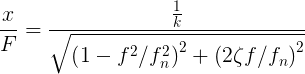
где
![]()
![]() называется коэффициентом демпфирования.
называется коэффициентом демпфирования.
Из последних 2 уравнений можно видеть, что, когда частота воздействующей силы близка к резонансной частоте, податливость определяется только слагаемым, содержащим коэффициент затухания, и, как результат, податливость может быть довольно большой. Когда частота силы, вызывающей вибрации равна резонансной частоте стержня (то есть f ≈ fn), каждый максимум скорости вынуждающей вибрации совпадает с максимумом ускорения возбуждаемой вибрации. В результате вынуждающая вибрация увеличивает ускорение стержня, что накапливает вибрационную энергию, что, в свою очередь, приводит к усилению вынуждающей вибрации.
Другой способ изобразить резонанс в этом примере - рассмотреть, что происходит, когда частоту функции вынуждающей силы медленно увеличивают с нуля. Когда частота близка к нулю, стержень изгибается синхронно с вынуждающей силой. Когда частота увеличивается, стержень будет отставать от вынужденной вибрации, потому что он не может мгновенно менять направление в ответ на периодические изменения направления приложенной силы (то есть вибрации). Фазовая задержка будет увеличиваться с частотой, как показано на рисунке 3. На резонансной частоте фазовая задержка между колебанием стержня и принудительной вибрацией будет ровно 90°, что означает, что максимум в ускорении стержня всегда совпадает с максимумом в скорости вибрации. В результате происходит усиление вибрационного входа (см. Рис. 2 и 3).
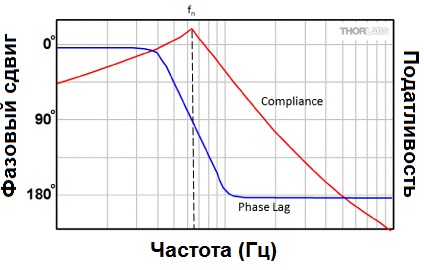
Рисунок 3: Изменение фазовой задержки между возбужденными и вынужденными колебаниями для системы с одним резонансом
При частотах вынужденных колебаний, превышающих резонансную частоту, разность фаз между принудительными и возбужденными колебаниями в этой теоретической однорезонансной системе составляет 180°.
В реальной системе, такой как оптический стол, существует много возможных резонансных мод колебаний. Фаза возбуждаемой вибрации зависит от места на столе, на котором производится измерение, а также от типа возбуждаемой вибрации.
Податливость на высоких частотах
На более высоких частотах податливость полностью зависит от массы (инерции) стола. Для f >> fn, уравнение податливости может быть аппроксимирована как
![]()
где m - эффективная масса, а f - частота вынуждающей силы.
В некоторых очень простых колебательных системах, таких как одна масса, подвешенная на пружине, довольно легко оценить массу, участвующую в вибрации. Однако в реальных системах массовый вклад в общем уравнении податливости может стать довольно сложным. Например, структура оптического стола такова, что он имеет несколько типов резонансных режимов вибрации. Поэтому разные точки на столе испытывают разные амплитуды вибрации. В узловых точках вообще нет амплитуды колебаний для этого конкретного узла колебаний. В результате эффективная масса, участвующая в вибрации, представляет собой сложную функцию, которая обычно определяется численно.
Изменение резонансной частоты
Резонансная частота зависит от жесткости и массы объекта. Уменьшение массы и / или увеличение жесткости сдвигает резонанс к более высокой частоте, как видно на рисунке 4. Увеличение массы и / или уменьшение жесткости сдвигает резонансную частоту ниже.
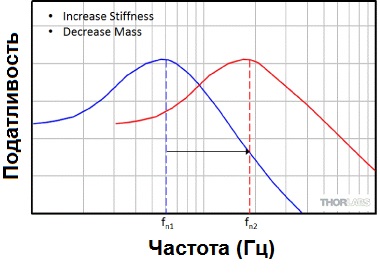
Рисунок 4: Смещение резонансной частоты при изменении отношения жесткости к массе
Баланс между массой и жесткостью является простой, но важной концепцией в конструкции оптического стола, потому что это позволяет сдвигать резонансы оптического стола к более высоким частотам с более низкими амплитудами. Понятно, что это можно сделать, просто увеличив жесткость стола. Однако если это сопровождается пропорциональным увеличением массы, то резонансы не будут смещены. Чтобы повысить резонансную частоту, жесткость должна быть максимизирована при минимизации массы.
