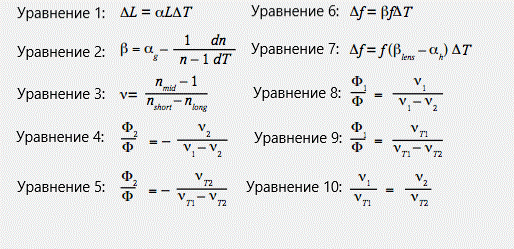Введение в пассивную атермализацию
Для приложений, подверженных колебаниям температуры, важно разработать атермальную оптическую систему: оптическую систему, которая нечувствительна к тепловым изменениям окружающей среды и возникающей в результате дефокусировке системы. Разработка атермальной конструкции, которая зависит от коэффициента теплового расширения (КТР) материалов и изменения индекса с температурой (dn/dT), особенно важна в инфракрасном диапазоне. Значение dn/dT большинства ИК-материалов на порядки выше, чем у стекол для видимого диапазона, что приводит к большим изменениям показателя преломления. Кроме того, хотя оптические системы часто проектируются в воздухе, материал корпуса также чувствителен к тепловым изменениям, и это следует учитывать при рассмотрении атермальной конструкции.
Тепловая расфокусировка
Расширение и сжатие материала из-за изменений температуры регулируется коэффициентом теплового расширения материала α, который измеряется в единицах 10-6 м/°C (или ppm/°C). Изменение длины (L) материала из-за изменения температуры определяется уравнением 1.
Тепловая дефокусировка – это изменение положения точки фокуса на оси при изменении температуры из-за изменения показателя преломления с температурой (dn/dT) и расширения материала. Аналогичное уравнение, количественно определяющее изменение фокусного расстояния линзы в воздухе в зависимости от температуры, дается уравнением 2, где β – термооптический коэффициент.
Термооптический коэффициент β можно определить с помощью уравнения 3, где αg – КТР стекла. Уравнение для β должно включать член для изменения показателя преломления воздуха в зависимости от температуры, но, поскольку этот член мал по сравнению со значениями dn/dT материала в ИК-диапазоне, он здесь не включен. Это приближение не следует использовать в видимом диапазоне, поскольку воздействие воздуха больше влияет на термооптический коэффициент, чем в ИК диапазоне.
Для объектива, установленного в корпусе с коэффициентом теплового расширения αh, изменение положения точки фокуса представляет собой комбинацию изменения фокусного расстояния объектива и изменения положения плоскости изображения из-за расширения корпуса, как показано в уравнении 4. Если изменение длины корпуса равно изменению фокусного расстояния из-за линзы, то расфокусировка равна нулю, и система считается атермальной.
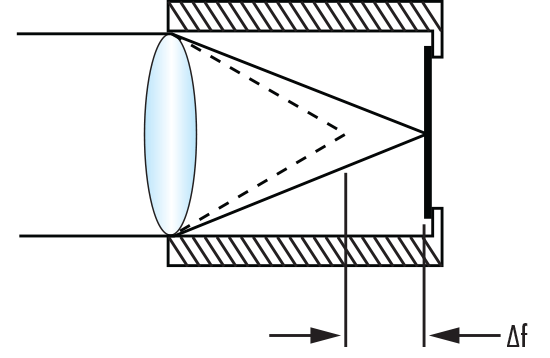
Расфокусировка (Δf) линзы в металлическом корпусе при изменении температуры (ΔT)
Уравнения ахроматических и атермальных дублетов
Распространенным оптическим элементом является ахроматический дублет, в котором для коррекции цвета используются положительные и отрицательные элементы из разных материалов с равными и противоположными количествами хроматической аберрации. Предполагая, что элемент находится в воздухе, коэффициент дисперсии ν для произвольного диапазона волн, определяемого самой длинной, самой короткой и средней длиной волны, дается уравнением 5. Если условия уравнений 6 и 7 удовлетворяются, результатом является ахроматический дублет. Оптимальное решение – это решение, содержащее два элемента с наибольшей разностью ν: Δν.
Чем больше Δν, тем больше фокусное расстояние (меньшая мощность) и меньшие радиусы (уменьшаются аберрации и улучшаются оптические характеристики). Посмотрев на график стекол, легко визуально выбрать крон и бесцветное стекло, у которых есть большая разница в ν. Аналогичным образом, можно использовать обратный термооптический коэффициент, обычно называемый тепловым числом ν, в ахроматических уравнениях для создания атермального дублета (уравнения 8 и 9). Если спроектировать дублет, в котором выполняются условия уравнений ахроматического дублета и атермального дублета (уравнения 6-9), результатом будет ахротермальная система: система, которая одновременно является ахроматической и атермальной (уравнение 10).
Построив график зависимости теплового коэффициента ν (νT) от цветового коэффициента ν, можно визуально идентифицировать два материала, которые можно использовать для разработки ахротермальной системы. Учитывая уравнение для прямой (y = mx + b, где m – наклон, а b – точка пересечения по оси Y), видно, что если установить точку пересечения по оси y равной нулю и выбрать материал (ν1, νT1), то наклон равен m = νT1/ν1. Из уравнения ахротермального дублета известно, что чтобы наклон двух разных материалов был одинаковым, чтобы добиться цветокоррекции и атермализации; любые два материала, которые могут быть соединены линией, проходящей через источник, обеспечат ахротермальное решение. Стекла IG5 и AMTIR1 обеспечат почти ахротермальное решение в воздухе для LWIR (8–12 мкм). Примечание: График не учитывает расширение какого-либо механического корпуса системы.
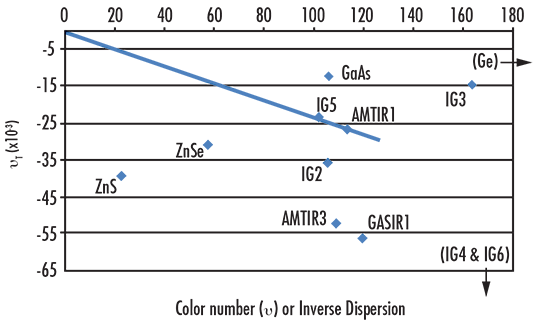
Образец графика νT в зависимости от ν для дальней ИК области (8-12 мкм)
Графический метод выбора ахротермального стекла и материалов корпуса
Альтернатива графику зависимости теплового коэффициента ν (νT) от цветового коэффициента ν заключается в построении графика зависимости термооптического коэффициента (β) от обратного цветового коэффициента ν. Этот метод не только помогает идентифицировать два доступных оптических материала, но также помогает определить КТР материала корпуса, необходимого для ахротермального решения. Точка пересечения по оси Y обеспечивает необходимый материал корпуса через линию, которая проходит через два материала и пересекает ось Y. В случае, если один материал корпуса с требуемым КТР недоступен, он может быть достигнут с использованием биметаллического корпуса или альтернативного решения для механического монтажа.
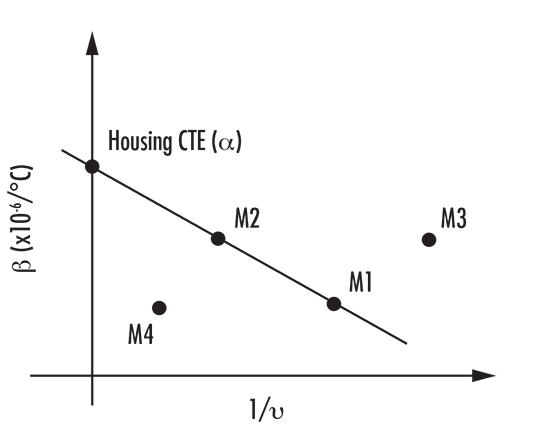
График атермальных стекол, отображающий β в зависимости от (1/ν)
Важно отметить, что этот метод по-прежнему предполагает, что dn/dT воздуха меньше, чем у оптических материалов; в то время как это верно для инфракрасных систем, dn/dT воздуха необходимо учитывать для систем, работающих в видимом спектре.